Abstract
Logical graphs are next presented as a formal system by going back to the initial elements and developing their consequences in a systematic manner.
Formal Development
Logical Graphs : 1 gives an informal introduction to the initial elements of logical graphs, and hopefully provides the reader with an intuitive sense of their motivation and rationale.
The next order of business is to give the exact forms of the axioms that are used in the following more formal development, devolving from Peirce’s various systems of logical graphs via Spencer-Brown’s Laws of Form (LOF). In formal proofs, a variation of the annotation scheme from LOF will be used to mark each step of the proof according to which axiom, or initial, is being invoked to justify the corresponding step of syntactic transformation, whether it applies to graphs or to strings.
Axioms
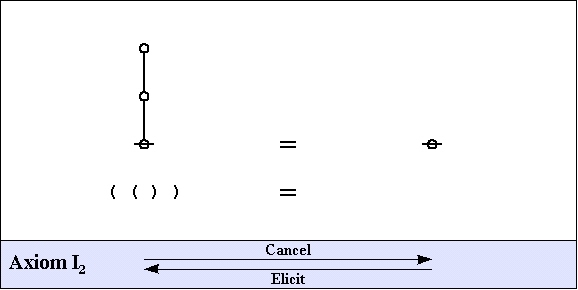
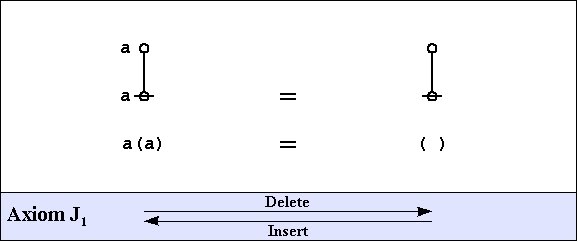
The axioms are just four in number, divided into the arithmetic initials, I1 and I2, and the algebraic initials, J1 and J2.
| (20) | |
| (21) | |
| (22) | |
| (23) |
One way of assigning logical meaning to the initial equations is known as the entitative interpretation (EN). Under EN, the axioms read as follows:
| I1 | : | true or true | = | true |
| I2 | : | not true | = | false |
| J1 | : | a or not a | = | true |
| J2 | : | (a or b) and (a or c) | = | a or (b and c) |
Another way of assigning logical meaning to the initial equations is known as the existential interpretation (EX). Under EX, the axioms read as follows:
| I1 | : | false and false | = | false |
| I2 | : | not false | = | true |
| J1 | : | a and not a | = | false |
| J2 | : | (a and b) or (a and c) | = | a and (b or c) |
All of the axioms in this set have the form of equations. This means that all of the inference steps that they allow are reversible. The proof annotation scheme employed below makes use of a double bar ====== to mark this fact, although it will often be left to the reader to decide which of the two possible directions is the one required for applying the indicated axiom.
Frequently Used Theorems
The actual business of proof is a far more strategic affair than the simple cranking of inference rules might suggest. Part of the reason for this lies in the circumstance that the usual brands of inference rules combine the moving forward of a state of inquiry with the losing of information along the way that doesn’t appear to be immediately relevant, at least, not as viewed in the local focus and the short run of the moment to moment proceedings of the proof in question. Over the long haul, this has the pernicious side-effect that one is forever strategically required to reconstruct much of the information that one had strategically thought to forget in earlier stages of the proof, if “before the proof started” can be counted as an earlier stage of the proof in view.
This is just one of the reasons that it can be very instructive to study equational inference rules of the sort that our axioms have just provided. Although equational forms of reasoning are paramount in mathematics, they are less familiar to the student of the usual logic textbooks, who may find a few surprises here.
By way of gaining a minimal experience with how equational proofs look in the present forms of syntax, let us examine the proofs of a few essential theorems in the primary algebra.
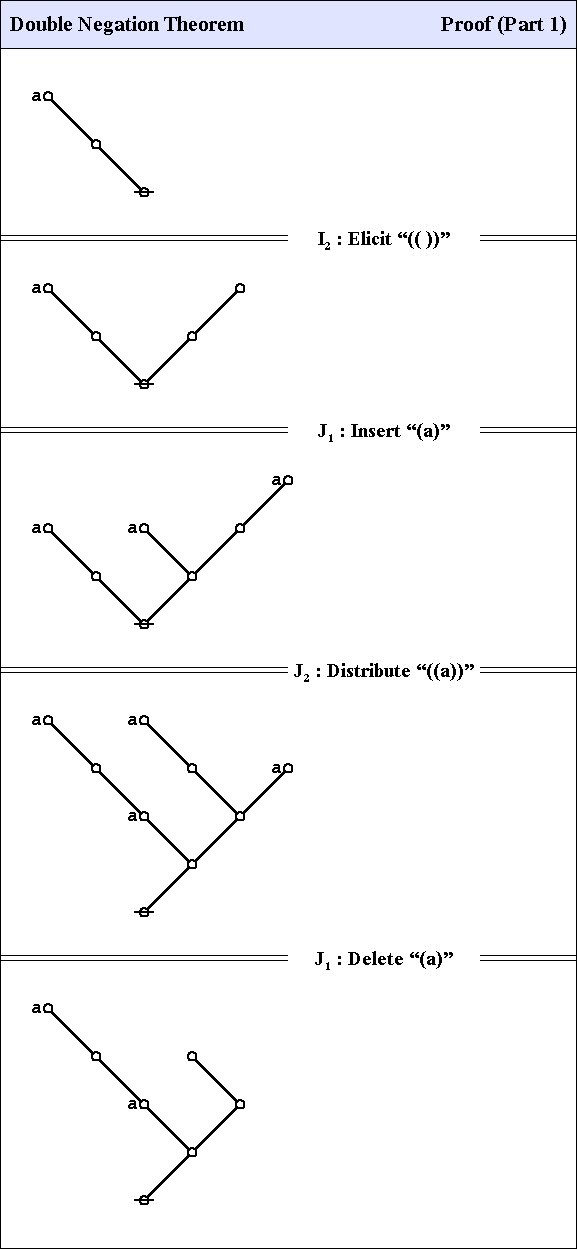
C1. Double Negation Theorem
The first theorem goes under the names of Consequence 1 (C1), the double negation theorem (DNT), or Reflection.
| (24) |
The proof that follows is adapted from the one that was given by George Spencer Brown in his book Laws of Form (LOF) and credited to two of his students, John Dawes and D.A. Utting.
| (25) |
| (26) |
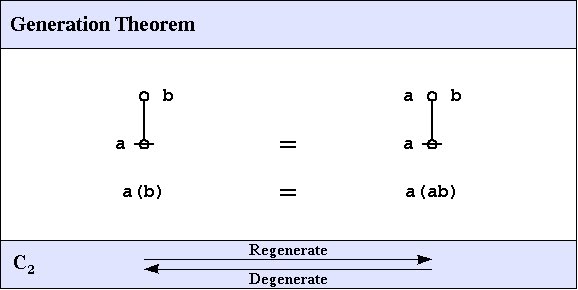
C2. Generation Theorem
One theorem of frequent use goes under the nickname of the weed and seed theorem (WAST). The proof is just an exercise in mathematical induction, once a suitable basis is laid down, and it will be left as an exercise for the reader. What the WAST says is that a label can be freely distributed or freely erased anywhere in a subtree whose root is labeled with that label. The second in our list of frequently used theorems is in fact the base case of this weed and seed theorem. In LOF, it goes by the names of Consequence 2 (C2) or Generation.
| (27) |
Here is a proof of the Generation Theorem.
| (28) |
C3. Dominant Form Theorem
The third of the frequently used theorems of service to this survey is one that Spencer-Brown annotates as Consequence 3 (C3) or Integration. A better mnemonic might be dominance and recession theorem (DART), but perhaps the brevity of dominant form theorem (DFT) is sufficient reminder of its double-edged role in proofs.
| (29) |
Here is a proof of the Dominant Form Theorem.
| (30) |
Exemplary Proofs
Using no more than the axioms and theorems recorded so far, it is possible to prove a multitude of much more complex theorems. A couple of all-time favorites are listed below.